Are you a student in Karnataka who is looking for comprehensive KSEEB 2nd PUC Maths Chapter 1 Relations and Functions Ex 1.4 Solutions? Look no further! In this page, you will get accurate solutions tailored for your academic needs, making learning simple and effective.
These solutions align with the syllabus of the Karnataka Secondary Education Examination Board (KSSEB), ensuring you have the right guidance. Each step is explained in an easy-to-understand manner, helping you grasp the concepts of Relations and Functions without any confusion.
The KSEEB 2nd PUC Maths Chapter 1 Relations and Functions Ex 1.4 Solutions provided here include detailed explanations for every question. This approach not only builds your problem-solving skills but also boosts your confidence for exams.
In this page, you will find reliable and clear KSEEB 2nd PUC Maths Chapter 1 Relations and Functions Ex 1.4 Solutions, designed to make your study experience stress-free. Use these solutions to enhance your understanding and excel in your mathematics preparation.
Karnataka 2nd PUC Maths Question Bank Chapter 1 Relations and Functions Ex 1.4
2nd PUC Maths Relations and Functions NCERT Text Book Questions and Answers Ex 1.4
Question 1.
Determine whether or not each of the definition of given below gives a binary operation. In the event that is not a binary operation, give justification for this.
(i) On Z+, * define by a * b = a – b
Answer:
2 ∈ Z+, 5 ∈ Z+, 2 – 5 = -3 ∉ Z+
hence not a binary operation.
(ii) On Z+, define * by a * b =ab
Answer:
∀ a ∈ Z+, b ∈ Z+ ab ∈ Z+, hence a * b ∈ Z+
∴ * is a binary operation.
(iii) On R, define * by a*b = ab2
Answer:
a ∈ R, b ∈ R then ab2 ∈ R
∴ a*b ∈ R
∴ * is a binary operation.
(iv) On Z+, define * by a * 6 = |a – b|
Answer:
a ∈ Z+, b ∈ Z+, |a – b| ∈ Z+
∴ a * b ∈ Z+
∴ * is a binary operation.
(v) On Z+, define* by a * b = a
Answer:
a ∈ Z+, b ∈ Z+ then a ∈ Z+
∴ a * b ∈ Z+
∴ * is a binary operation.
Question 2.
For each binary * operation defined below,determine * whether is commutative or associative.
(i) On Z, define a * b = a – b
Answer:
a = 3, b = 2, a – b = 3 – 2= 1
b-a = 2-3 = -1
a – b ≠ b – a, hence not commutative
a = 3, b = 2, c = 1
(a * b) * c = (3 – 2) * 1 = 1 * 1 = 0
a*(b * c) = 3* (2 * 1) = 3*(2 – 1) = 3 * 1 = 3 – 1 = 2
(a * b) * c ≠ a * (b * c), hence * is not associative
(ii) On Q, define a*b = ab + 1
Ans:
a ∈ Q, b ∈ Q
a * b = ab + 1
b * a = ab + 1
∴ a * b = b * a, hence commutative ( a * b )*c = (ab+1) *c
= (ab + 1) c + 1 = abc + c + 1
a*(b*c) = a* (bc + 1)
= a (bc + 1) + 1 = abc + a + 1
∴ (a * b) *c * a* (b * c)
hence * is not associative
(iii) On Q,define a∗b=ab/2
Answer:
(iv) On Z+, define a*b = 2“*
Answer:
a g Z+, be Z+,
a*b = 2ab
b * a = 2ba = 2ab a * b = b * a
hence * is commutative
(a * b) * c = 2ab * c = 2ab * c = 22al’x‘
a*(b*c) = a* 2ac = 2a–2“
hence (a * b) * c * a * (b * c)
.: * is not Associative.
(v) On Z+, define a * b = ab
Answer:
a ∈ Z+, b ∈ Z+, a * b = ab
b * a = ba
a * b ≠ b * a, hence * is not commutative
(a * b) * c = ab * c = (ab)c = abc
a* (b * c) = a * bc = (a)bc
(a * b) * c ≠ a* (b * c)
hence * is not associative.
(vi) On R – {- 1}, define a∗b=a/b+1
Answer:
Question 3.
Consider the binary ∧ operation on the set {1, 2, 3, 4, 5} defined by a ∧ b = min {a, b}. Write the operation table of the operation ∧
Answer:
| ∧ | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 2 | 2 | 2 |
| 3 | 1 | 2 | 3 | 3 | 3 |
| 4 | 1 | 2 | 3 | 4 | 4 |
| 5 | 1 | 2 | 3 | 4 | 5 |
Question 4.
Consider a binary * operation on the set {1, 2, 3, 4, 5} given by the following multiplication table (Table 1.2).
(i) Compute (2 * 3) * 4 and 2 * (3 * 4)
(ii) * Is commutative?
(iii) Compute (2 * 3)*(4 * 5).
(Hint: use the following table)
Table 1.2
| * | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 1 | 2 | 1 |
| 3 | 1 | 1 | 3 | 1 | 1 |
| 4 | 1 | 2 | 1 | 4 | 1 |
| 5 | 1 | 1 | 1 | 1 | 5 |
Answer:
(i) (2 * 3) * 4 = 1 * 4= 1
2 * (3 * 4) = 2 * 1 = 1
(ii) Since the table is symmetric with main diagonal it is commutative.
(iii) (2 * 3) * (4 * 5) = 1 * 1 = 1.
Question 5.
*’Let be the binary operation on the set {1, 2, 3, 4, 5} defined by a *’ b = H.C.F. of a and b. Is the *’ operation same as the * operation defined in Exercise 4 above? Justify your answer.
Answer:
a, b ∈ {1,2, 3,4, 5}, a* b = H.C.F. of a and b we composition table for *’
| *’ | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 1 | 2 | 1 |
| 3 | 1 | 1 | 3 | 1 | 1 |
| 4 | 1 | 2 | 1 | 4 | 1 |
| 5 | 1 | 1 | 1 | 1 | 5 |
Both the composition tables are exactly same hence the operation* and *’ are same.
Question 6.
Let* be the binary operation on N given by a * b = L.C.M. of a and Find
(i) 5 * 7, 20 * 16
(ii) * Is commutative?
(iii) * Is associative?
(iv) Find the identity of * in N
(v) Which elements of N are invertible for the operation* ?
Answer:
(i) 5 *7 = L.C.M. of 5, 7 = 35
20 *16 = L.C.M. of 20, 16 = 80.
(ii) a * b = L.C.M. of (a, b) = L.C.M. (b,a)
= b * a
hence * is commutative.
(iii) (a * b) * c = L.C.M. of a, b, c
a* (b*c) = L.C.M. of a, b, c
hence * is associative.
(iv) Let ‘e’ be the identity element, than
a * e = e * a = a ∀ a ∈ N
L.C.M. (a, e) = L.C.M. (e, a) = a
⇒ e divides a ∀a ∈N
⇒ e = 1
∴ 1 is the identity element.
(v) Let a ∈ N be invertible.
∴ be N such that a * b = b * a = L.C.M. (a, b) = 1
⇒ a = 1, b = 1
∴ only invertible element in N is 1

Question 7.
Is * defined on the set {1, 2, 3, 4, 5} by a * b = L.C.M. of a and b a binary operation? Justify your answer.
Answer:
L.C.M. of 3, 5 = 15
3 * 5 = L.C.M. of (3, 5) = 15 g {1,2, 3,4,5}
hence * is not a binary operation.
Question 8.
Let * be the binary operation on N defined by a * b = H.C.F. of a and b. Is * commutative? Is * associative? Does there exist identity for this binary operation on N?
Answer:
a ∈ N, b ∈ N, a ∈ b = H.C.F. of a and b
= H.C.F. of b and a = b * a
hence * is commutative
a ∈ N, b ∈ N, e ∈ N.
a* (b * e) = H.C.F. a, b, c
= (a * b) * c * is associative.
Let e ∈ N be the identity element
a * e = e * a = a
H.C.F. a and e = a
∴ a divides e ∀ a ∈ N
which is not possible as there does not exist such a number e, which is divisible by every number.
∴ identity element does not exist.
Question 9.
Let * be a binary operation on the set Q of rational numbers as follows. Find which of the binary operations are commutative and which are associative.
(i) a * b = a – b
Answer:
a * b = a – b,∀ a> be Q
a * b = a – b * a = b – a a * b ≠ b * a
hence not commutative
(a * b) * c = (a – b) * c = a – b – c
a* (b * c) = a* (b – c) = a – (b – c) = a – b + c ≠ (a* b) * c
hence ≠ is not associative
(ii) a * b = a2 + b2
Answer:
a, b ∈ Q ⇒ a * b = a2 + b2
= b2 + a2 = b * a
hence * is commutative
(a * b) * c = (a2 + b2) * c2 = (a2 + b2)2 + c2
a*(b * c) = a* (b2 + c2) = a2 + (b2 + c2)2
hence * is not associative
(iii) a * b = a + ab
Answer:
a * b = a + ab
b * a = b + ab ∴ a * b ≠ b * a,
hence * is not commutative
(a * b) * c = (a + ab) * c = (a + ab) + (a + ab) c
= a + ab + ac + abc
a* (b * c) = a * (b + bc)
= a + a (b + bc)
= a + ab + bca
≠ (a * b) * c
hence * is not associative
(iv) a * b = (a – b)2
Answer:
a * b = (a – b)2 = (b – a)2= b * a
hence * is not commutative
(a * b) * c = (a – b)2 * c = ((a-b)2 – c)2 = (a – b)4+ c2 – 2c (a – b)2
a*(b * c) = a* (b – c)2 = [a -(b – c)]2 = a2 + (b – c)2 – 2a (b – c)2
hence not associative
(v) a∗b=ab/4
Answer: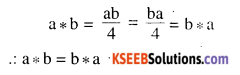
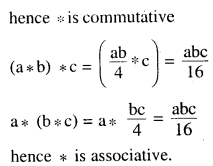
(vi) a*b = ab2
Answer:
a ∈ Q, be Q , a * b = ab2
b * a = ba2 ∴ a * b≠ b * a
hence not commutative.
(a * b) * c = (ab2) * c = ab2c2
a * (b * c) = a * (bc2) = ab2c4
(a * b) * c = a * (b)
∴ * is not associative.
Question 10.
Show that none of the operations given above has identity.
(i) Let ‘e’ be the identity in Q such that
Answer:
a * e = e * a = a
a – e = a = e – a
⇒ e = 0 or e = 2a ∀ a ∈ Q
which is not possible. Hence no identity.
(ii) a * b = a2 + b2
Answer:
Let e ∈ Q be the identity element
a * e = a2 + e2 =a e * a = c2 + a2 = a
which is not possible as a2 ≠ a ∀ a ∈ Q
hence identity element doesn’t exist.
(iii) a*b = a + ab
Answer:
Let e ∈ Q be the identity element
a * e = a + ae = a ⇒ ae = 0, ⇒ e = 0
e * a = e + ae = a ⇒ e=a/1+a
∴e=0 and e=a/1+a ∀a∈Q which is not possible. Hence identity element does not exist.
(iv) a * b = (a – b)2
Answer:
Let e be the identity element
a * e = (a – e)2 = a
e * a = (e – a)2 = a
∴ a – e = ≠ a, e – a = ± a
⇒ e = 0 and e = 2a ∀ a ∈ Q which is not possible.
Hence no identity element.
(v) a∗b=ab/4
Answer:
Let e be the identity element
a∗e=ae/4=a and e∗a=ea/4=a
∴ e = 4
∴ 4 is the identity element.
(vi) a*b = ab2
Answer:
Let e be the identity element
a * e = ae2 = a
e * a = ea2 = a
∴e2=1 and e=1a∀a∈Q
which is not possible. Hence identity element does not exist.
Question 11.
Let A = N x N and * be the binary operation on A defined by (a, b)* (c, d) = (a + c, b + d) Show that is commutative and associative. Find the identity element for * on A, if any. Answer:
(a, b) * (c,d) = (a + c, b + d)
= (c + a, d + b) = (c, d) * (a, b)
hence commutative
[(a,b) * (c,d)] * (e, f) = (a + c, b + d) * (e, f) = (a + c + e, b + d + f) = (a, b) * [(c,d) * (e, f)] hence * is associative.
Let (e, f) be the identity element of A
(e, f) * (a, b) = (a,b) * (c, f) = (a, b)
(a + e, b + 0 = (a, b) ⇒ (e = 0, f = 0) ∉ N
hence no identity element.
Question 12.
State whether the following statements are true or false. Justify.
(i) For an arbitrary binary operation * on a set N, a * a = a ∀ a ∈ N.
Answer:
If a * b = a+ b, then
a * a = a + a = 2a ≠ a
∴ statement is false
(ii) If * is a commutative binary operation N, then a*(b*c) = (c*b) * a
Answer:
Since commutative a* (b*c) = (b*c) *a
= (c *b) * a
hence true.
(iii) For every binary operation defined on a set having exactly one element a is necessarily commutative and associative .with a as the identity element and a being the inverse of a.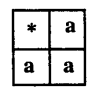
Answer:
A = {a}
* : A x A → A defined by a* a = a ∀ a ∈ A Also from the table it is commutative and associative. Also a is the identity element and also inverse of a .
Question 13.
Consider a binary operation * on N defined as a * b = a3 + b3. Choose the
(A) *Is both associative and commutative?
(B) *Is commutative but not associative?
(c) *Is associative but not commutative?
(D) *Is neither commutative nor associative?
Answer:
a*b = a3 + b3 = b3 + a3 = b*a
hence commutative
(a*b) * c = (a3 + b3) *c = (a3 + b3)3 + c3
a * (b * c) = a * (b3 + c3) = a3 + (b3 + c3)3
hence not associative
“B “ is the correct answer.
Conclusion: KSEEB 2nd PUC Maths Chapter 1 Relations and Functions Ex 1.4 Solutions
In conclusion, the solutions provided for KSEEB 2nd PUC Maths Chapter 1 Relations and Functions Ex 1.4 offer a comprehensive understanding of the topic. By utilizing these solutions, students can effectively solve complex problems and further enhance their mathematical skills. To access the complete set of solutions and ensure success in this chapter, it is recommended to refer to the KSEEB 2nd PUC Maths Chapter 1 Relations and Functions Ex 1.4 Solutions.
